Vediamo tutto quello che c’è da sapere su Maurits Cornelis Escher, l’artista che è riuscito a sconvolgere lo spazio
Il 17 giugno 1898 nacque Maurits Cornelis Escher, un artista ancora oggi celebrato come uno dei maggiori incisori e grafici del secolo passato, e forse della storia stessa. Le forme uniche, le geometrie intricate e le architetture sorprendenti dei suoi lavori rappresentano tuttora eccellenti esempi di connubio tra arte e matematica. È notevole che i suoi capolavori abbiano ricevuto plauso soprattutto da matematici, logici e fisici, i quali trovavano nei suoi disegni echeggiati gli equilibri delicati e le formule caratteristiche del loro ambito di studio. Le forme paradossali presenti nelle opere di Escher ci immergono in mondi misteriosi ma irresistibilmente coinvolgenti. Ma vediamo tutto quello che c’è da sapere sulle opere di Escher.
L’universo, la matematica e i mondi impossibili: ecco cosa rappresentano le opere di Escher
Escher crea illusioni ottiche sfruttando gli effetti percettivi basati sulle leggi della Gestalt, una corrente psicologica tedesca del secolo scorso. La sua opera, prevalentemente composta da xilografie, litografie e mezzetinte, esplora la geometria, la cristallografia e la percezione visiva. Escher, visionario dello spazio, ci invita a osservare la natura da un nuovo punto di vista, stimolando la nostra curiosità. Nato nelle Fiandre e trasferitosi in Italia nel 1923, Escher si ispira ai paesaggi italiani e alle opere medievali e rinascimentali, oltre a riflettere sullo spazio come gli artisti del Novecento. Il suo lavoro si distingue per le rappresentazioni con punti di vista multipli e simultanei, che uniscono influssi storici e contemporanei. Ma vediamo quali sono i mondi che Escher ha rappresentato nei suoi quadri.
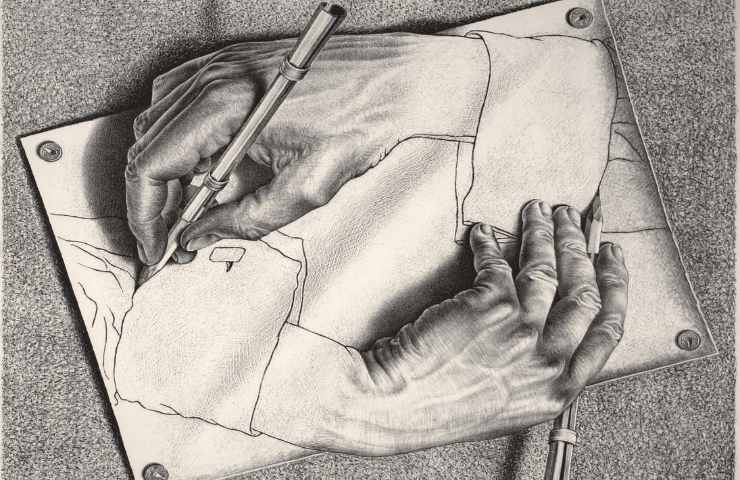
Il mondo ideale e il mondo reale
Da Platone ed Euclide in poi, la filosofia e la scienza hanno sempre affiancato un ordine ideale alla realtà tangibile. Questa necessità non è solo concettuale e matematica, ma anche etica ed esistenziale. Tuttavia, il rapporto tra i due è spesso problematico, poiché rappresentano mondi distinti e incommensurabili. Sebbene la matematica sia un potente strumento per comprendere il mondo fisico e, in parte, quello biologico, finora ha avuto meno successo nell’interpretare i fenomeni cognitivi e psicologici. Escher esplora costantemente il confine tra ordine mentale e disordine reale, cercando di inserire un senso di ordine nella caoticità vitale che l’uomo-artista sperimenta costantemente nel mondo esterno.
Le figure nello spazio
Un esempio di questa interazione tra filosofia e arte si ritrova nelle opere ispirate alla tassellazione geometrica dello spazio, che consiste nella copertura di una superficie con figure geometriche regolari ripetute in modo periodico. Questo compito può essere relativamente semplice quando si tratta di rivestire una superficie regolare, ma diventa più complesso quando si cerca di piastrellare una struttura curva come un arco o una volta. Diventa ancora più arduo se cerchiamo di rappresentare in termini matematici i contorni irregolari di una costa o le forme di una nuvola.
Il limite del cerchio
In certi contesti, la geometria euclidea pianeggiante deve cedere il passo a una geometria curva, come nella teoria della relatività generale di Einstein, la quale però non si adatta bene ai nostri schemi percettivi euclidei. L’opera di Escher “Limite del cerchio” potrebbe sembrare un semplice cerchio bidimensionale, ma in realtà rappresenta uno spazio iperbolico in cui le linee parallele formate da figure di pesci congruenti si addensano all’orizzonte e convergono all’infinito. La nostra percezione ci fa vedere le figure affollarsi e rimpicciolire ai margini, ma è un’illusione euclidea: cambiando il nostro punto di vista, possiamo immaginare di trovarci ai confini del cerchio, osservando la realtà come se fossimo al suo centro e, muovendoci in ogni direzione, ritrovando sempre gli stessi rapporti di grandezza che si ripetono all’infinito. Il “cerchio” di Escher, infatti, rappresenta lo spazio curvo dell’universo, chiuso in sé stesso, un universo finito ma senza limiti, essenzialmente la rappresentazione limitata dell’infinito, simile alla sfera perfetta di Parmenide e all’universo di Einstein. Emerge così un’altra ossessione filosofica costante nelle opere di Escher: la tensione dialettica tra la “rappresentazione” limitata della realtà e la possibilità dell’infinito, non idealizzata come un’espansione del finito in una dimensione superiore, bensì come il limite angoscioso che condanna l’essere umano, come Sisifo, a ripetere infinitamente lo sforzo di esistere, tornando eternamente al punto di partenza.

Metamorfosi nello-dello spazio
Il problema della tassellazione dello spazio, che consiste nel rivestire una superficie con poligoni regolari in modo ricorsivo e periodico, si confronta con sfide geometriche complesse, specialmente con poligoni irregolari come i pentagoni. Esiste un interesse crescente per affrontare questo problema tramite la teoria dei gruppi, che si concentra sulle simmetrie dei gruppi di figure anziché sulle singole tessere, offrendo un approccio creativo e inventivo. Escher, affascinato da questo problema (e notevolmente influenzato dal fatto che suo fratello fosse un cristallografo), esplora il lato misterioso del processo creativo, cercando di reinventare il mondo scoprendo le sue leggi nascoste. Le sue opere, come le metamorfosi e la litografia Rettili, mostrano trasformazioni spaziali partendo da arabeschi o mosaici, creando forme viventi che fluttuano tra dimensioni geometriche e organiche, riflettendo il perenne ciclo della vita e della morte.
Lo scienziato e l’artista
Vale la pena esaminare l’aspetto creativo del lavoro di Escher, che condivide caratteristiche fondamentali con l’impresa scientifica. La scienza, infatti, non nasce semplicemente dall’osservazione passiva della realtà, ma dall’anticipazione di modelli teorici che forniscono una struttura ipotetica per predire e cercare conferme sperimentali. Un esempio di questa struttura congetturale-ipotetica della scienza è offerto dal neo-premio Nobel Giorgio Parisi.
Uno dei suoi contributi più significativi riguarda lo studio dei sistemi caotici, come il vetro, la cui struttura disordinata contrasta con quella cristallina. Parisi ha sviluppato un modello semplice, il modello di Sherrington-Kirkpatrick, costituito da magneti con due sole direzioni – Nord e Sud – collegati in modo casuale. Da questa rete casuale di interazioni magnetiche emergono comportamenti inaspettati, simili a quelli del vetro. Questo dimostra come un modello teorico possa collegare la complessità materiale della natura alla nostra comprensione.
Questo approccio ipotetico-deduttivo e creativo avvicina la scienza a una dimensione speculativa, fondata su audaci congetture che sfidano la complessità del mondo reale, nella speranza che la temerarietà teorica premi gli audaci ricercatori. Questo riflette il significato della celebre frase di Einstein: “La cosa più incomprensibile al mondo è che esso sia comprensibile”. Escher si muove in questa prospettiva, lavorando pazientemente al confine tra il caos della realtà e l’ordine della mente, cercando con cura e quasi alchemicamente il tassello (o il sistema di tasselli) con cui ricostruire e interpretare la complessità mutevole dell’Universo, inclusa la sua stessa mente di artista.






